伯努利分布指的是对于随机变量X有, 参数为p(0

伯努利分布只有两种可能的结果，1(成功)和0(失败)。因此，具有伯努利分布的随机变量X可以取值为1，也就是成功的概率，可以用p来表示，也可以取值为0，即失败的概率，用q或1-p来表示。

概率质量函数由下式给出：px(1-p)1-x， 其中x € (0, 1)。它也可以写成：

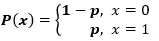
成功与失败的概率不一定相等。这里，成功的概率(p)与失败的概率不同。所以，下图显示了我们之间比赛结果的伯努利分布。

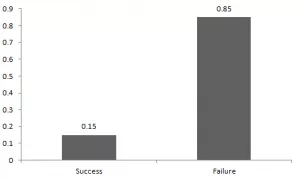
这里，成功的概率 = 0.15，失败的概率 = 0.85 。如果我打了你，我可能会期待你向我打回来。任何分布的基本预期值是分布的平均值。来自伯努利分布的随机变量X的期望值如为：

E(X) = 1p + 0(1-p) = p 

随机变量与二项分布的方差为： 

V(X) = E(X²) – [E(X)]² = p – p² = p(1-p)

伯努利分布的例子有很多，比如说明天是否要下雨，如果下雨则表示成功，如果不下雨，则表示失败。